2831. Find the Longest Equal Subarray 🟠 05-23-2024
Description:
You are given a 0-indexed integer array nums and an integer k.
A subarray is called equal if all of its elements are equal. Note that the empty subarray is an equal subarray.
Return the length of the longest possible equal subarray after deleting at most k elements from nums.
A subarray is a contiguous, possibly empty sequence of elements within an array.
Example 1:
Input: nums = [1,3,2,3,1,3], k = 3 Output: 3 Explanation: It's optimal to delete the elements at index 2 and index 4. After deleting them, nums becomes equal to [1, 3, 3, 3]. The longest equal subarray starts at i = 1 and ends at j = 3 with length equal to 3. It can be proven that no longer equal subarrays can be created.
Example 2:
Input: nums = [1,1,2,2,1,1], k = 2 Output: 4 Explanation: It's optimal to delete the elements at index 2 and index 3. After deleting them, nums becomes equal to [1, 1, 1, 1]. The array itself is an equal subarray, so the answer is 4. It can be proven that no longer equal subarrays can be created.
Constraints:
1 <= nums.length <= 1051 <= nums[i] <= nums.length0 <= k <= nums.length
Ideas After analyze we find for each element with same value, we can use sliding window to calculate the max num that meet the constraints. So basically for each distinct value, we need a sliding window.
- traverse the array get the map, then for each key in map, do a sliding window
0 1 2 3 4 5 6
1 3 2 3 1 3 1 k = 3
i
j
map<value, list of index>
map: {
1 : 0 4 6
3 : 1 3 5
2 : 2
}
we can use list to store index, and use two int stand for the boundary. or a simple way -> use queue.pop to update the boundary.
- We find the above solution need traverse the array two times in total. Is there a simple way to calculate while traversing the array?
In a queue, how to determine if new added element is satisfied? answer is : (index - queue.peekFirst() + 1) - queue.size() > k ? (index - queue.peekFirst() + 1) stand for the length between the first and last occurance of the element. To calculate the rest number of elements who’s value are not euqlas to the current value, we use length - number of current value in between, compare it with the k. if greater than k, that means it can not be replaced within k times. then we need to pop the first element out of the queue and check again until it is satisfied. Then we update the globalmax.
Solution
class Solution {
public int longestEqualSubarray(List<Integer> nums, int k) {
int globalMax = Integer.MIN_VALUE;
Map<Integer, Deque<Integer>> map = new HashMap<>();
for (int i = 0; i < nums.size(); i++) {
// add it to the map
Deque<Integer> queue = map.computeIfAbsent(nums.get(i), num -> new ArrayDeque<>());
queue.offerLast(i);
// update the boundary
while(i - queue.peekFirst() + 1 - queue.size() > k) {
queue.pollFirst();
}
globalMax = Math.max(globalMax, queue.size());
}
return globalMax;
}
}
447. Number of Boomerangs 🟠 01-08-2024
Description:
You are given n points in the plane that are all distinct, where points[i] = [xi, yi]. A boomerang is a tuple of points (i, j, k) such that the distance between i and j equals the distance between i and k (the order of the tuple matters).
Return the number of boomerangs.
Example 1:
Input: points = [[0,0],[1,0],[2,0]] Output: 2 Explanation: The two boomerangs are [[1,0],[0,0],[2,0]] and [[1,0],[2,0],[0,0]].
Example 2:
Input: points = [[1,1],[2,2],[3,3]] Output: 2
Example 3:
Input: points = [[1,1]] Output: 0
Constraints:
n == points.length1 <= n <= 500points[i].length == 2-104 <= xi, yi <= 104- All the points are unique.
Ideas:
When we first see this problem, we can easily come up with a brute force solution. We can use three for loops to find the boomerangs. But the time complexity will be O(n^3).
Another way to solve this problem is : for each point, use a hashmap to store the distance between this point and other points. Then we know how many points have the same distance to this point.
For point A, if there exists n points have the same distance to A, that means we can pick any two of n points to form a boomerang. So the total number of boomerangs is n * (n - 1).
With this idea, we can for loop the entryset of the map and calculate the total number of boomerangs of one point and sum of all points.
Solution:
class Solution {
public int numberOfBoomerangs(int[][] points) {
if (points.length < 3) return 0;
int res = 0;
// for each point, calculate the distance between this point and other points
for (int[] p : points) {
Map<Integer, Integer> map = new HashMap<>();
for (int[] q : points) {
int dis = (p[0] - q[0]) * (p[0] - q[0]) + (p[1] - q[1]) * (p[1] - q[1]);
map.put(dis, map.getOrDefault(dis, 0) + 1);
}
// for each point, calculate the total number of boomerangs
for (Map.Entry<Integer, Integer> e : map.entrySet()) {
int m = e.getValue();
res += m * (m - 1);
}
}
return res;
}
}
356. Line Reflection 🟠 01-08-2024
Description:
Given n points on a 2D plane, find if there is such a line parallel to the y-axis that reflects the given points symmetrically.
In other words, answer whether or not if there exists a line that after reflecting all points over the given line, the original points' set is the same as the reflected ones.
Note that there can be repeated points.
Example 1:

Input: points = [[1,1],[-1,1]] Output: true Explanation: We can choose the line x = 0.
Example 2:

Input: points = [[1,1],[-1,-1]] Output: false Explanation: We can't choose a line.
Constraints:
n == points.length1 <= n <= 104-108 <= points[i][j] <= 108
Follow up: Could you do better than O(n2)?
Ideas:
Since we only reflect Y axis, to find the line, we can easily get the line with the leftmost and rightmost points. Then we can use a hashset to store the points. Then we can check if the reflected points are in the hashset.
Solution:
class Solution {
// Here we create a new class Point to store the x and y value, and override the equals and hashCode method
class Point {
double x;
double y;
Point(double x, double y) {
this.x = x;
this.y = y;
}
@Override
public boolean equals(Object o) {
if (this == o) return true; // check reference
// check null and class type
if (o == null || getClass() != o.getClass()) return false;
// cast o to Point
Point point = (Point) o;
return point.x == this.x && point.y == this.y;
}
@Override
public int hashCode() {
return Objects.hash(x, y);
}
}
public boolean isReflected(int[][] points) {
if (points.length == 1) return true;
Set<Point> pointSet = new HashSet<>();
double min = Integer.MAX_VALUE;
double max = Integer.MIN_VALUE;
for (int[] point : points) {
max = Math.max(point[0], max);
min = Math.min(point[0], min);
pointSet.add(new Point(point[0], point[1]));
}
// Here 2 * (line - point[0]) + point[0] is the reflected point, we don't need to consider the point is at the left or right of the line
double line = min + (max - min) / 2;
for (int[] point : points) {
if (!pointSet.contains(new Point(2 * (line - point[0]) + point[0], point[1]))) return false;
}
return true;
}
}
146. LRU Cache 🟠 01-07-2024
Description:
Design a data structure that follows the constraints of a Least Recently Used (LRU) cache.
Implement the LRUCache class:
LRUCache(int capacity)Initialize the LRU cache with positive sizecapacity.int get(int key)Return the value of thekeyif the key exists, otherwise return-1.void put(int key, int value)Update the value of thekeyif thekeyexists. Otherwise, add thekey-valuepair to the cache. If the number of keys exceeds thecapacityfrom this operation, evict the least recently used key.
The functions get and put must each run in O(1) average time complexity.
Example 1:
Input
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
Output
[null, null, null, 1, null, -1, null, -1, 3, 4]
Explanation
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // cache is {1=1}
lRUCache.put(2, 2); // cache is {1=1, 2=2}
lRUCache.get(1); // return 1
lRUCache.put(3, 3); // LRU key was 2, evicts key 2, cache is {1=1, 3=3}
lRUCache.get(2); // returns -1 (not found)
lRUCache.put(4, 4); // LRU key was 1, evicts key 1, cache is {4=4, 3=3}
lRUCache.get(1); // return -1 (not found)
lRUCache.get(3); // return 3
lRUCache.get(4); // return 4
Constraints:
1 <= capacity <= 30000 <= key <= 1040 <= value <= 105- At most
2 * 105calls will be made togetandput.
Ideas:
- We can use a Doubly Linked List to store the key and value. Head -> A -> B -> C -> D -> Tail With this we can easily remove the tail and add a new node to the head. But the problem is to find the node in the list. We can use a HashMap to store the key and the node. So we can easily find the node in the list. HashMap: key -> Node. So the time complexity for get and put is O(1).
class LRUCache {
class DoubledListNode {
int key;
int value;
DoubledListNode prev;
DoubledListNode next;
DoubledListNode(int key, int value) {
this.key = key;
this.value = value;
}
}
// initialize the cache
Map<Integer, DoubledListNode> cache = new HashMap<>();
int capacity;
int size;
DoubledListNode head, tail;
public LRUCache(int capacity) {
this.capacity = capacity;
this.size = 0;
this.head = new DoubledListNode(-1, -1);
this.tail = new DoubledListNode(-1, -1);
head.next = tail;
tail.prev = head;
}
public int get(int key) {
}
public void put(int key, int value) {
}
}
- With the structure above, we can focus on the get and put method.
public int get(int key) {
// if the key is not in the cache, return -1
// if the key is in the cache, return the value and move the node to the head
// summary : we need a method moveToHead(DoubledListNode node)
// for this method, it contains two steps:
// 1. remove the node from the list -> removeNode(node)
// 2. add the node to the head -> addNewNodeToHead(node)
}
public void put(int key, int value) {
// if the key is in the cache, update the value and move the node to the head
// if the key is not in the cache, add the node to the head, if the size is greater than capacity, remove the tail
// summary : we need a method moveToHead(DoubledListNode node) and addNewNodeToHead(DoubledListNode node) and evictTail()
}
- Implement the methods above
private void moveToHead(DoubledListNode node) {
// remove the node from the list
removeNode(node);
// add the node to the head
addNewNodeToHead(node);
}
private void removeNode(DoubledListNode node) {
node.prev.next = node.next;
node.next.prev = node.prev;
}
private void addNewNodeToHead(DoubledListNode node) {
node.next = head.next;
node.prev = head;
// remember to update the head and the previous node next to head
head.next.prev = node;
head.next = node;
}
private void evictTail() {
DoubledListNode tailNode = tail.prev;
removeNode(tailNode);
return tailNode;
}
- Implement the Get and Put methods
public int get(int key) {
if (!cache.containsKey(key)) return -1;
DoubledListNode node = cache.get(key);
moveToHead(node);
return node.value;
}
public void put(int key, int value) {
if (cache.containsKey(key)) {
DoubledListNode node = cache.get(key);
node.value = value;
moveToHead(node);
} else {
DoubledListNode node = new DoubledListNode(key, value);
cache.put(key, node);
addNewNodeToHead(node);
size++;
if (size > capacity) {
DoubledListNode tailNode = evictTail();
cache.remove(tailNode.key);
size--;
}
}
}
- the final solution
class LRUCache {
class DoubledListNode {
int key;
int value;
DoubledListNode prev;
DoubledListNode next;
DoubledListNode(int key, int value) {
this.key = key;
this.value = value;
}
}
Map<Integer, DoubledListNode> cache = new HashMap<>();
int capacity;
int size;
DoubledListNode head, tail;
public LRUCache(int capacity) {
this.capacity = capacity;
this.size = 0;
this.head = new DoubledListNode(-1, -1);
this.tail = new DoubledListNode(-1, -1);
head.next = tail;
tail.prev = head;
}
public int get(int key) {
DoubledListNode node = cache.get(key);
// not exist -> return -1
if (node == null) return -1;
// exist, move node to head, return value;
moveToHead(node);
return node.value;
}
public void put(int key, int value) {
// if exist, update value, move to head
DoubledListNode node = cache.get(key);
if (node != null) {
node.value = value;
moveToHead(node);
} else {
DoubledListNode newNode = new DoubledListNode(key, value);
cache.put(key, newNode);
addNewNodeToHead(newNode);
size++;
if (size > capacity) {
DoubledListNode tailNode = evictTail();
this.size--;
cache.remove(tailNode.key);
}
}
// not exist, add a new node to head (update map), check if exceed capacity? evict tail node
}
private void moveToHead(DoubledListNode node) {
// break current node prev and next
removeNode(node);
// move to head
addNewNodeToHead(node);
}
private void addNewNodeToHead(DoubledListNode node) {
node.prev = head;
node.next = head.next;
// **
head.next.prev = node;
head.next = node;
}
private DoubledListNode evictTail() {
DoubledListNode tailNode = tail.prev;
removeNode(tailNode);
return tailNode;
}
private void removeNode(DoubledListNode node) {
node.prev.next = node.next;
node.next.prev = node.prev;
}
}
2558. Take Gifts From the Richest Pile 🟢 10-26-2023
2558. Take Gifts From the Richest Pile
Description:
You are given an integer array gifts denoting the number of gifts in various piles. Every second, you do the following:
- Choose the pile with the maximum number of gifts.
- If there is more than one pile with the maximum number of gifts, choose any.
- Leave behind the floor of the square root of the number of gifts in the pile. Take the rest of the gifts.
Return the number of gifts remaining after k seconds.
Example 1:
Input: gifts = [25,64,9,4,100], k = 4 Output: 29 Explanation: The gifts are taken in the following way: - In the first second, the last pile is chosen and 10 gifts are left behind. - Then the second pile is chosen and 8 gifts are left behind. - After that the first pile is chosen and 5 gifts are left behind. - Finally, the last pile is chosen again and 3 gifts are left behind. The final remaining gifts are [5,8,9,4,3], so the total number of gifts remaining is 29.
Example 2:
Input: gifts = [1,1,1,1], k = 4 Output: 4 Explanation: In this case, regardless which pile you choose, you have to leave behind 1 gift in each pile. That is, you can't take any pile with you. So, the total gifts remaining are 4.
Constraints:
1 <= gifts.length <= 1031 <= gifts[i] <= 1091 <= k <= 103
Ideas: Each time, we need to pick the maximum of the array, and push the new value back to the array. So we can use a priority queue to solve this problem.
Solution:
class Solution {
public long pickGifts(int[] gifts, int k) {
PriorityQueue<Integer> pq = new PriorityQueue<>(gifts.length, (e1, e2) -> e2 - e1);
pq.addAll(Arrays.stream(gifts).mapToObj(Integer::valueOf).collect(Collectors.toList()));
// do not know addAll is heapify the array?
while (k-- > 0) {
pq.offer((int) Math.sqrt(pq.poll()));
}
long res = 0;
while (!pq.isEmpty()) {
res += pq.poll();
}
return res;
}
}
Time complexity: O(n + klogn) where n is the length of the gifts array
Space complexity: O(n)
1465. Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts 🟠 10-27-2023
1465. Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts
Description:
You are given a rectangular cake of size h x w and two arrays of integers horizontalCuts and verticalCuts where:
horizontalCuts[i]is the distance from the top of the rectangular cake to theithhorizontal cut and similarly, andverticalCuts[j]is the distance from the left of the rectangular cake to thejthvertical cut.
Return the maximum area of a piece of cake after you cut at each horizontal and vertical position provided in the arrays horizontalCuts and verticalCuts. Since the answer can be a large number, return this modulo 109 + 7.
Example 1:
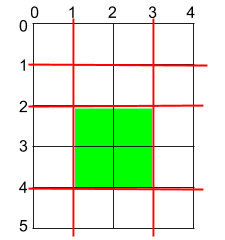
Input: h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3] Output: 4 Explanation: The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green piece of cake has the maximum area.
Example 2:
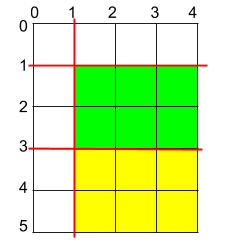
Input: h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1] Output: 6 Explanation: The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green and yellow pieces of cake have the maximum area.
Example 3:
Input: h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3] Output: 9
Constraints:
2 <= h, w <= 1091 <= horizontalCuts.length <= min(h - 1, 105)1 <= verticalCuts.length <= min(w - 1, 105)1 <= horizontalCuts[i] < h1 <= verticalCuts[i] < w- All the elements in
horizontalCutsare distinct. - All the elements in
verticalCutsare distinct.
Original Ideas:
The first idea I got is calculate the intervals for horizontal and vertical cuts. Then do a for loop to find the maximum area. But this solution is not efficient enough. The time complexity is O(n^2) where n is the length of the horizontalCuts or verticalCuts.
Ideas:
Based on the original ideas, we analyze the problem and find that we only need to find the maximum interval for horizontalCuts and verticalCuts. So we can sort the horizontalCuts and verticalCuts and find the maximum interval for horizontalCuts and verticalCuts. Then we can get the maximum area by multiply the maximum interval for horizontalCuts and verticalCuts.
Solution:
class Solution {
private final int MOD = 100000007;
public int maxArea(int h, int w, int[] horizontalCuts, int[] verticalCuts) {
Arrays.sort(horizontalCuts);
Arrays.sort(verticalCuts);
// here is another hard part, to convert long to int. For these problems that need mod 10e9 + 7, if we do not need time operation, we can use int, otherwise we need to use long
return (int) (findMaxInterval(horizontalCuts, h) * findMaxInterval(verticalCuts, w) % 1000000007);
}
public long findMaxInterval(int[] array, int length){
int res = 0, pre = 0;
for (int i = 0; i < array.length; i++) {
res = Math.max(array[i] - pre, res);
pre = array[i];
}
return (long) Math.max(res, length - pre);
}
}
Time complexity: O(nlogn) where n is the length of horizontalCuts or verticalCuts (sorting)
Space complexity: O(1)
2520. Count the Digits That Divide a Number 🟢 10-26-2023
2520. Count the Digits That Divide a Number
Description:
Given an integer num, return the number of digits in num that divide num.
An integer val divides nums if nums % val == 0.
Example 1:
Input: num = 7 Output: 1 Explanation: 7 divides itself, hence the answer is 1.
Example 2:
Input: num = 121 Output: 2 Explanation: 121 is divisible by 1, but not 2. Since 1 occurs twice as a digit, we return 2.
Example 3:
Input: num = 1248 Output: 4 Explanation: 1248 is divisible by all of its digits, hence the answer is 4.
Constraints:
1 <= num <= 109numdoes not contain0as one of its digits.
Ideas:
The best way to do it is using the modulo operation. If convert to String, the space complexity will be O(n) where n is the length of the string. If we use modulo operation, the space complexity will be O(1).
Solution:
class Solution {
public int countDigits(int num) {
int t = num;
int res = 0;
while (t != 0) {
if (num % (t % 10) == 0) {
res++;
}
t /= 10;
}
return res;
}
}
Time complexity: O(logn) where n is the number.
Space complexity: O(1)
2698. Find the Punishment Number of an Integer 🟠 10-25-2023
2698. Find the Punishment Number of an Integer
Description:
Given a positive integer n, return the punishment number of n.
The punishment number of n is defined as the sum of the squares of all integers i such that:
1 <= i <= n- The decimal representation of
i * ican be partitioned into contiguous substrings such that the sum of the integer values of these substrings equalsi.
Example 1:
Input: n = 10 Output: 182 Explanation: There are exactly 3 integers i that satisfy the conditions in the statement: - 1 since 1 * 1 = 1 - 9 since 9 * 9 = 81 and 81 can be partitioned into 8 + 1. - 10 since 10 * 10 = 100 and 100 can be partitioned into 10 + 0. Hence, the punishment number of 10 is 1 + 81 + 100 = 182
Example 2:
Input: n = 37 Output: 1478 Explanation: There are exactly 4 integers i that satisfy the conditions in the statement: - 1 since 1 * 1 = 1. - 9 since 9 * 9 = 81 and 81 can be partitioned into 8 + 1. - 10 since 10 * 10 = 100 and 100 can be partitioned into 10 + 0. - 36 since 36 * 36 = 1296 and 1296 can be partitioned into 1 + 29 + 6. Hence, the punishment number of 37 is 1 + 81 + 100 + 1296 = 1478
Constraints:
1 <= n <= 1000
Ideas:
After we analyze the problem, we can find the hard part is to cut the number into contiguous substrings. To get different combination of numbers, we can use DFS to solve this.
Solution:
public int punishmentNumber(int n) {
int sum = 0;
for (int i = 1; i <= n; i++) {
if (canPartitioned(String.valueOf(i*i), i, 0, 0)) sum += i * i;
}
return sum;
}
public boolean canPartitioned(String num, int target, int index, int sum) {
if (index == num.length()) {
return sum == target;
}
// here we do not have the choice to pick nothing, so the index start from index + 1
// add [index, i) substring to the sum
for (int i = index + 1; i <= num.length(); i++) {
// here we can do a early termination if the sum is greater than target
if (canPartitioned(num, target, i, sum + Integer.parseInt(num.substring(index, i)))) return true;
}
return false;
}
Time complexity: non-polynomial time complexity since DFS is used
Space complexity: O(n * len(i*i)) where n is the input and len(i*i) is the length of the square of i (the maximum length is 2 * len(n)), so the space complexity is O(n * len(n))
1155. Number of Dice Rolls With Target Sum 🟠 10-24-2023
1155. Number of Dice Rolls With Target Sum
Description:
You have n dice, and each die has k faces numbered from 1 to k.
Given three integers n, k, and target, return the number of possible ways (out of the kn total ways) to roll the dice, so the sum of the face-up numbers equals target. Since the answer may be too large, return it modulo 109 + 7.
Example 1:
Input: n = 1, k = 6, target = 3 Output: 1 Explanation: You throw one die with 6 faces. There is only one way to get a sum of 3.
Example 2:
Input: n = 2, k = 6, target = 7 Output: 6 Explanation: You throw two dice, each with 6 faces. There are 6 ways to get a sum of 7: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1.
Example 3:
Input: n = 30, k = 30, target = 500 Output: 222616187 Explanation: The answer must be returned modulo 109 + 7.
Constraints:
1 <= n, k <= 301 <= target <= 1000
Ideas: We can use dynamic programming to solve this problem. DP[n][t] represents the number of possible ways to roll n dices, so the sum of the face-up numbers equals t.
We have the transition function:
DP[n][t] = ∑ (DP[n - 1][t - j]) where j is from 1 to k && t - j >= 0
Solution:
class Solution {
private static final int MOD = 1000000007;
public int numRollsToTarget(int n, int k, int target) {
int[][] DP = new int[n + 1][target + 1];
// min of k and target (corner case will cause index out of bound)
int min = k > target ? target : k;
// initilization the base case
for (int i = 1; i <= min; i++) {
DP[1][i] = 1;
}
// DP bottom up
for (int i = 2; i < n + 1; i++) {
// start with DP[i][i] because when t < i, it is impossible to roll i dices and get the sum of t
for (int t = i; t < target + 1; t++) {
for (int j = 1; j <= k; j++) {
if (t - j >= 0) DP[i][t] = (DP[i][t] + DP[i - 1][t - j]) % MOD;
}
}
}
return DP[n][target];
}
}
Time complexity: O(n * k * target)
Space complexity: O(n * target)
2678. Number of Senior Citizens 🟢 10-23-2023
2678. Number of Senior Citizens
Description:
You are given a 0-indexed array of strings details. Each element of details provides information about a given passenger compressed into a string of length 15. The system is such that:
- The first ten characters consist of the phone number of passengers.
- The next character denotes the gender of the person.
- The following two characters are used to indicate the age of the person.
- The last two characters determine the seat allotted to that person.
Return the number of passengers who are strictly more than 60 years old.
Example 1:
Input: details = ["7868190130M7522","5303914400F9211","9273338290F4010"] Output: 2 Explanation: The passengers at indices 0, 1, and 2 have ages 75, 92, and 40. Thus, there are 2 people who are over 60 years old.
Example 2:
Input: details = ["1313579440F2036","2921522980M5644"] Output: 0 Explanation: None of the passengers are older than 60.
Constraints:
1 <= details.length <= 100details[i].length == 15details[i] consists of digits from '0' to '9'.details[i][10] is either 'M' or 'F' or 'O'.- The phone numbers and seat numbers of the passengers are distinct.
Ideas:
This is a simple problem, the only thing we need to do is to extract the age from the string and compare it with 60.
Solution:
class Solution {
public int numOlderThan60(String[] details) {
int res = 0;
for (String detail : details) {
// extract the age from the string using substring, instead of using character and ascii code to manually calculate the age like this : Integer.valueOf(str.charAt(11) - '0') * 10 + Integer.valueOf(str.charAt(12) - '0');
int age = Integer.parseInt(detail.substring(10, 12));
if (age > 60) res++;
// or we can only compare the 11th character with '6' to check if the age is greater than 60
}
return res;
}
}
Class Solution {
// using Stream API only for Java 8 and above
public int numOlderThan60(String[] details) {
return (int)Arrays.stream(details).filter(string -> Integer.valueOf(string.substring(11,13)) > 60).count();
}
}
Time complexity: O(n)
Space complexity: O(1)
1402. Reducing Dishes 🔴 10-22-2023
Description:
A chef has collected data on the satisfaction level of his n dishes. Chef can cook any dish in 1 unit of time.
Like-time coefficient of a dish is defined as the time taken to cook that dish including previous dishes multiplied by its satisfaction level i.e. time[i] * satisfaction[i].
Return the maximum sum of like-time coefficient that the chef can obtain after preparing some amount of dishes.
Dishes can be prepared in any order and the chef can discard some dishes to get this maximum value.
Example 1:
Input: satisfaction = [-1,-8,0,5,-9] Output: 14 Explanation: After Removing the second and last dish, the maximum total like-time coefficient will be equal to (-1*1 + 0*2 + 5*3 = 14). Each dish is prepared in one unit of time.
Example 2:
Input: satisfaction = [4,3,2] Output: 20 Explanation: Dishes can be prepared in any order, (2*1 + 3*2 + 4*3 = 20)
Example 3:
Input: satisfaction = [-1,-4,-5] Output: 0 Explanation: People do not like the dishes. No dish is prepared.
Constraints:
n == satisfaction.length1 <= n <= 500-1000 <= satisfaction[i] <= 1000
Ideas:
The intuition behind this approach is that we always try to maximize the like-time coefficient by prioritizing dishes with higher satisfaction.
To get the maximum like-time coefficient, apparently all non-negative satisfaction dishes should be included. The rest is how to deal with negative satisfaction dishes.
First we sort the array in ascending order and iterate from back to front. [-9, -8, -1, 0, 5] when it comes to -1, now the dishes we pick is [0, 5] and the sum is 5, each time we add a new dishes, the satisfaction level will increase by sum of all previous selected dishes and the current dishes (here is - 1 + 0 + 5 = 4) which is sum + satisfaction[i]. if sum + satisfaction[i] is less than 0, we can stop the iteration because the rest dishes will be less than 0. If sum + satisfaction[i] is greater than 0, we can add it to the result.
To record the result, we can use a variable res to record the result, each time we pick a new dishes, the result will increase sum + satisfaction[i]. We don’t need to record the list of the dishes and calculate the sum by times[i] * satisfaction[i].
Solution:
We can use a greedy approach. We start by sorting the satisfaction array in descending order. Then, we iterate over the array and keep accumulating the satisfaction until the accumulated value is greater than zero. At each step, we update our result.
class Solution {
public int maxSatisfaction(int[] satisfaction) {
int sum = 0;
int res = 0;
Arrays.sort(satisfaction);
for (int i = satisfaction.length - 1; i >= 0; i--) {
if (satisfaction[i] < 0 && sum + satisfaction[i] < 0) break;
sum += satisfaction[i--];
res += sum;
}
return res;
}
}
Time complexity: O(nlogn)
Space complexity: O(1)
3254. Find the Power of K-Size Subarrays I 🟢 11-08-2024
You are given an array of integers nums of length n and a positive integer k.
The power of an array is defined as:
- Its maximum element if all of its elements are consecutive and sorted in ascending order.
- -1 otherwise.
You need to find the power of all nums of size k.
Return an integer array results of size n - k + 1, where results[i] is the power of nums[i..(i + k - 1)].
Example 1:
Input: nums = [1,2,3,4,3,2,5], k = 3
Output: [3,4,-1,-1,-1]
Explanation:
There are 5 subarrays of nums of size 3:
[1, 2, 3]with the maximum element 3.[2, 3, 4]with the maximum element 4.[3, 4, 3]whose elements are not consecutive.[4, 3, 2]whose elements are not sorted.[3, 2, 5]whose elements are not consecutive.
Example 2:
Input: nums = [2,2,2,2,2], k = 4
Output: [-1,-1]
Example 3:
Input: nums = [3,2,3,2,3,2], k = 2
Output: [-1,3,-1,3,-1]
Constraints:
1 <= n == nums.length <= 5001 <= nums[i] <= 1051 <= k <= n
Solution:
- 合理转化题意,拆解 power 的定义,当连续且递增时才会取最大值。因为递增,最大值则是这个 subarray 的最右侧值。
- 因为题目以 length 为 k 的 subarray 进行拆解,所以应联想到用 sliding window 来解决
- 将 power 取值转化为逻辑实现:
- 连续递增 -> 前后差值为 1 -> 即 window block 内所有相邻 element 差值均为 1 时,条件成立
- 定义 cnt 为以 i 结尾连续递增的 element 个数,我们默认第 i 个数计入统计。cnt default = 1
- 第 i 个值,若跟 i-1 差值为 1 则 cnt++,(在 i-1 连续递增的数上+1,当前 i 也符合)若不为 1,则 cnt = 1 (从 i 重新开始,左边不连续递增,所以 i 为第一个符合的 element)
- 在遍历时,便有公式 cnt = nums[i] - nums[i - 1] == 1 ? cnt + 1 : 1;
-
考虑一开始第一个数没有左边,i - 1 越界了,则当 i==0 时默认为 1 – cnt = i == 0 nums[i] - nums[i - 1] != 1 ? 1 : cnt + 1; (当然也可以拆开写) - 因为左边可能都是递增的,所以 cnt>=k 代表向左 K 个肯定满足连续递增
class Solution {
public int[] resultsArray(int[] nums, int k) {
int n = nums.length;
int[] ans = new int[n - k + 1];
Arrays.fill(ans, -1);
int cnt = 0;
for (int i = 0; i = k) {
ans[i - k + 1] = nums[i];
}
}
return ans;
}
}
