leetcode 面经

BFS

690. Employee Importance

Binary search

875. Koko Eating Bananas

demo

875. Koko Eating Bananas

Solution :

Xx

TC : O(1)

SC : O(1)

Algorithm

690. Employee Importance

You have a data structure of employee information, including the employee's unique ID, importance value, and direct subordinates' IDs.

You are given an array of employees employees where:

• employees[i].id is the ID of the ith employee.
• employees[i].importance is the importance value of the ith employee.
• employees[i].subordinates is a list of the IDs of the direct subordinates of the ith employee.

Given an integer id that represents an employee's ID, return the total importance value of this employee and all their direct and indirect subordinates.

 

Example 1:

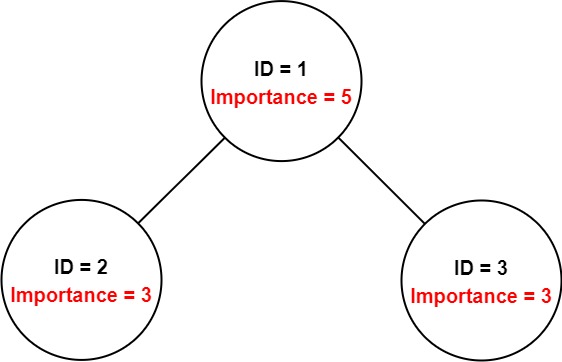
Input: employees = [[1,5,[2,3]],[2,3,[]],[3,3,[]]], id = 1
Output: 11
Explanation: Employee 1 has an importance value of 5 and has two direct subordinates: employee 2 and employee 3.
They both have an importance value of 3.
Thus, the total importance value of employee 1 is 5 + 3 + 3 = 11.

Example 2:

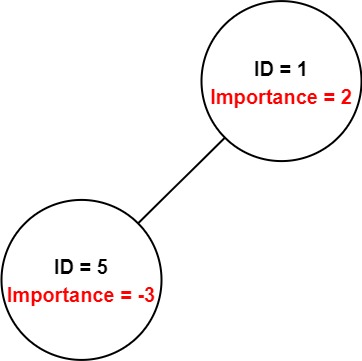
Input: employees = [[1,2,[5]],[5,-3,[]]], id = 5
Output: -3
Explanation: Employee 5 has an importance value of -3 and has no direct subordinates.
Thus, the total importance value of employee 5 is -3.

 

Constraints:

• 1 <= employees.length <= 2000
• 1 <= employees[i].id <= 2000
• All employees[i].id are unique.
• -100 <= employees[i].importance <= 100
• One employee has at most one direct leader and may have several subordinates.
• The IDs in employees[i].subordinates are valid IDs.

Solution: Use BFS and visited set to solve this problem, it is a typical BFS problem.

class Solution {
    public int getImportance(List<Employee> employees, int id) {
        // initialize map
        HashMap<Integer, Employee> map = new HashMap<>();
        for (Employee employee : employees) {
            map.put(employee.id, employee);
        }
        // this problem do not have a graph, visit does not need here
        HashSet<Employee> visit = new HashSet<>();
        Deque<Employee> queue = new ArrayDeque<>();
        Employee emp = getEmployeeById(map, id);
        int ip = 0;
        if (emp == null) return 0;
        queue.offerLast(emp);
        while (!queue.isEmpty()) {
            Employee cur = queue.pollFirst();
            if (visit.contains(cur)) continue;
            ip += cur.importance;
            for (Integer employeeId : cur.subordinates) {
                queue.offerLast(getEmployeeById(map, employeeId));
            }
            visit.add(cur);
        }
        return ip;
    }
    private Employee getEmployeeById(HashMap<Integer, Employee> map, int id) {
        if (map.containsKey(id)) return map.get(id);
        return null;
    }
}

TC : O(n) less than all employees

SC : O(n) map space

Solution2: DFS

class Solution {
    Map<Integer, Employee> map = new HashMap<Integer, Employee>();

    public int getImportance(List<Employee> employees, int id) {
        for (Employee employee : employees) {
            map.put(employee.id, employee);
        }
        return dfs(id);
    }

    public int dfs(int id) {
        Employee employee = map.get(id);
        int total = employee.importance;
        List<Integer> subordinates = employee.subordinates;
        for (int subId : subordinates) {
            total += dfs(subId);
        }
        return total;
    }
}

TC : O(n) less than all employees

SC : O(n) map space + call stack

875. Koko Eating Bananas

Solution : Binary search. This problem is hard to find that we could use binary search to solve this problem.

class Solution {
    public int minEatingSpeed(int[] piles, int h) {
        int left = 1;
        int right = Integer.MAX_VALUE;
        for (int pile : piles) {
            right = Math.max(right, pile);
        }
        // do a binary search here
        while (left < right - 1) {
            int mid = left + (right - left) / 2;
            if (getCount(piles, mid) <= h) {
                right = mid;
            } else {
                left = mid;
            }
        }
        return getCount(piles, left) <= h ? left : right;
    }
    private int getCount(int[] piles, int k) {
        int count = 0;
        for (int pile : piles) {
            count += pile / k;
            if (pile % k != 0) {
                count++;
            }
        }
        return count;
    }
}

TC : O(n * logn) --> O(n) for traverse the pile to getCount, O(logn) for binary search

SC : O(1)